Electrochemical cells exercises

title: Electrochemical cells exercises

A. The standard Gibbs energy change for the lead-acid battery is Δ_G_0 = -375.1 kJ/mol. What is the value you get if you use data from the table on page 391 in the textbook? Just summing up all the standard formation energies: PbO$_2$(s) + Pb(s) + 2HSO$_4^-$(aq) + 2H$_3$O$^+$(aq) $\leftrightarrow$ 2PbSO$_4$(s) + 4H$_2$O(l) -217.3 + 0 + 2*-755.9 + 2*-237.14 -(2*-813 + 4*-237.14) = 371.18 kJ/mol This is for charging.

B. On pages 58-59, the textbook explains pointwise how to calculate a cell voltage based on half cell reactions and tabulated standard data. This should be well known from physical chemistry. However, it is good to practice. The book, in footnote 309 suggests:

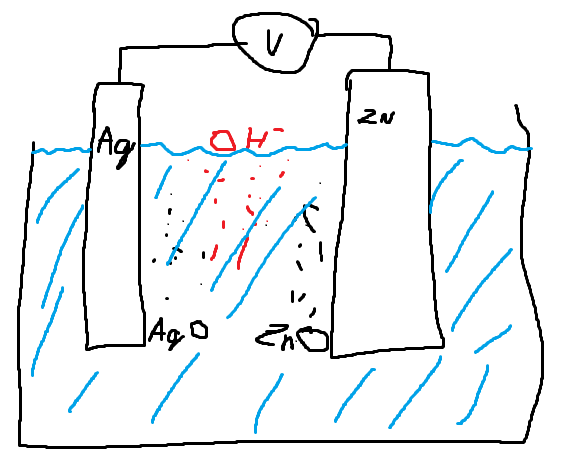
Using data from the Appendix, page 391 , follow this protocol to calculate the equilibrium voltage of the cell in which the electrode reactions are $\mathrm{Ag}_{2} \mathrm{O}(s)+\mathrm{H}_{2} \mathrm{O}(\ell)+2 \mathrm{e}^{-}(\mathrm{Ag}) \rightleftarrows 2 \mathrm{Ag}(\mathrm{s})+2 \mathrm{OH}^{-}(a q)$ and $\mathrm{ZnO}(s)+\mathrm{H}_{2} \mathrm{O}(\ell)+2 \mathrm{e}^{-}(\mathrm{Zn}) \rightleftarrows \mathrm{Zn}(s)+2 \mathrm{OH}^{-}(a q)$, reporting which of the electrodes is positive. Explain why the only data you need for this calculation are the standard Gibbs energies of silver oxide and zinc oxide. Compare you answers with those at Web#309.

What is Web#309? It is found in the textbook web resource at www.wiley.com/go/EST. Use this web resource to dive deeper into material you are interested in, or seek better explanations of.

Draw the cell, include copper wires to a voltmeter, and suggest how electrical potential lines may run through the cell in case of open circuit (no current running).

Book:

Write down equilibrium reactions at both electrodes separately, with electrons in on the left side
Make electron count match in both eqns, by doubling or tripling an equation.
Subtract eqn 2 from eqn 1, and calculate gibbs energy.
The potential difference will be: $\Delta E_{\mathrm{Iversus} \mathrm{II}}=\phi_{\mathrm{I}}-\phi_{\mathrm{II}}=-\frac{\Delta G}{n F} \quad$ cell voltage

–

As in the task
already done
$\mathrm{Ag}_{2} \mathrm{O}(s) - \mathrm{ZnO}(s) \leftrightarrow 2 \mathrm{Ag}(\mathrm{s}) - \mathrm{Zn}(s)$
$\mathrm{Ag}_{2} \mathrm{O}(s) + \mathrm{Zn}(s) \leftrightarrow \mathrm{ZnO}(s) + 2 \mathrm{Ag}(\mathrm{s})$, Gibbs energy: -11.2 - - 320.5 = 309.3
$\Delta E_{\mathrm{Iversus} \mathrm{II}}=-\frac{309.3\cdot 1000 J/mol}{2 \cdot 96485C/mol} = 1.6V$

C. Work two and two if possible. Explain the expressions to each other, ask questions, and discuss:

$v_{\mathrm{A}} \mathrm{A}+v_{\mathrm{B}} \mathrm{B}+\cdots \rightarrow v_{z} \mathrm{Z}+v_{\mathrm{Y}} \mathrm{Y}+\cdots$ $\exp \left\{\frac{-\Delta G^{\circ}}{R T}\right\}=\frac{a_{z}^{v_{z}} a_{Y}^{1_{Y}} \cdots}{a_{A}^{v_{\Lambda}} a_{B}^{v_{B}} \cdots}=K=\frac{\vec{k}}{\vec{k}} \quad$ equilibrium

$\exp \left\{\frac{n F}{R T} \Delta E^{\circ}\right\}=\exp \left\{\frac{-\Delta G^{\circ}}{R T}\right\}=K=\left(\frac{a_{Z}^{v_{z}} a_{\mathrm{Y}}^{v_{\mathrm{Y}}} \cdots}{a_{\mathrm{A}}^{v_{\mathrm{A}}} a_{\mathrm{B}}^{v_{\mathrm{B}}} \cdots}\right)_{\text {equilib }} \quad$ equilibrium

D. Draw a cell. Use the cell from B or the lead-acid cell, with potential lines under open circuit.

i) Indicate the direction of current in galvanic operation. The current leads to voltages (overpotentials) building up due to resistances in the electrolyte, interfaces (kinetics), and electrode phases. Are you able to include such voltages so that they all contribute to decrease the cell voltage?

Galvanic operation means discharging? If so, the electrical current goes from the cathode to the anode through the outer circuit. Thus the electron current goes the other way (from anode to cathode, or negatrode to positrode.) The overpotentials can be modeled by a small resistive load across each of the mentioned barriers. Is this the same as internal resistance?

ii) Indicate the direction of current in electrolytic operation. The current leads to voltages (overpotentials) building up due to resistances in the electrolyte, interfaces (kinetics), and electrode phases. Are you able to include such voltages so that they all contribute to increase the cell voltage?

Electrolytic operation: Charging, or inputing energy. This is the same as the one above? Internal resistance $\propto$ overpotential.

iii) In the graph below, the voltage changes from the OCV when current runs galvanically or electrolytically. Does this fit qualitatively with what you have been drawing in the previous two exercises?

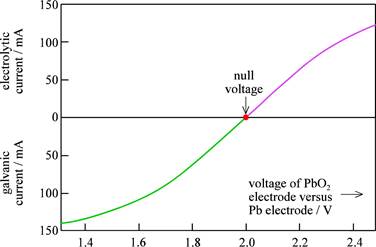
Only in the linear region, as if the internal resistances were purely a resistive load, the voltage increase would be linear with the current increase. However, on the figure we see that the current saturates at higher voltages, meaning that the resistance is actually increasing with current.

iv) A footnote in the textbook says about a cell at open circuit: “It can be argued that the cell is not at equilibrium; however, each of the electrodes is at equilibrium.” Discuss what is meant by this.

The cell in it self is at equilibrium when the voltage is zero, but the electrodes are in equilibrium since the charge densities and potentials are equaled out.(?)

E, The Daniell cell.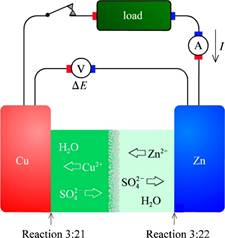

Self study and check: Eqs. 3.20-3.23 is standard from general and physical chemistry.

What goes on at the diaphragm under open circuit and galvanic conditions?

There is a liquid junction potential difference assicoiated with the porous diaphragm. This happens both under open curcuit and Galvanic operation.

Open Curcuit: Consentration of different ions can be different -> induces diffusion. If the diffusion is faster for one than the other, charge imbalance may occur. Ex: LiBr solved. Br$^-$ diffuses fast to the low consentration side of the diapragm, making that side negatively charged. It is opposed by charge, but it is sufficient for a noticable voltage.
Galvanic operation: The slowness of diffusion through the diaphragm probably makes the drain under-populated and the source overpopulated, creating a voltage difference across the diaphragm.

Express the Gibbs energy of each reactant and product of the total reaction in terms of standard Gibbs energy and activities, using the equations in the summary from Ch. 2. $$ G_{i}=G_{i}^{0}+R T \ln \left\{a_{i}\right\}=\left\{\begin{array}{l} G_{i}^{\circ} \text { pure solid, liquid or solvent of a dilute solution } \\ G_{i}^{\circ}+R T \ln \left\{p_{i} / p^{\circ}\right\} \text { gas except at very high pressure } \\ G_{i}^{\circ}+R T \ln \left\{c_{i} / c^{\circ}\right\} \text { nonionic solute in a dilute solution } \\ G_{i}^{\circ}+R T \ln \left\{\gamma_{i} c_{i} / c^{\circ}\right\} \text { ionic solute, even in dilute solution } \end{array}\right. $$ Reaction: $$ \mathrm{Cu}^{2+}(a q)+\mathrm{Zn}(s) \rightleftarrows \mathrm{Zn}^{2+}(a q)+\mathrm{Cu}(s) $$ $$\Delta G = \Delta G^\circ + RT ln \frac{\gamma c}{c^\circ} = 65.6 - (-147.2) kJ/mol + 24.38 L atm/mol*ln() = $$

Sum them to obtain the Gibbs energy change of the total reaction. Collect the standard energies to a standard Gibbs energy change for the reaction, and the activity terms to form the reaction quotient.

What is the cell voltage of the Daniell cell under standard conditions and what does standard conditions mean?

If we increase the concentration of solutions on both sides 10-fold, what happens with the cell voltage?

If you want to increase the cell voltage of a Daniell cell, how could you do that?

If you want to use a Daniell cell as an energy source, how could you assemble it to maximise the energy it can give?

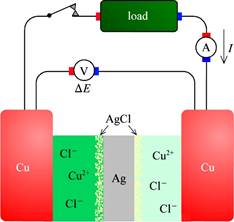
F. Bipolar electrodes

What goes on at the AgCl | Ag | AgCl “electrode”?

G. Bonus problem

Molecular oxygen cannot oxidize MnO2 to permanganate anions via the reaction

4MnO2(s) + 3O2(g) + 4OH- → 4MnO4-(aq) + 2H2O(l) E0cell = -0.20 V

Calculate the Ecell under non-standard conditions and decide if the oxidation will happen spontaneously or not when pH = 10, _p_O2 = 0.20 atm, [MnO4-] = 1∙10-4 M and T = 25 °C.