Electrochemical cells
Lead-acid cell
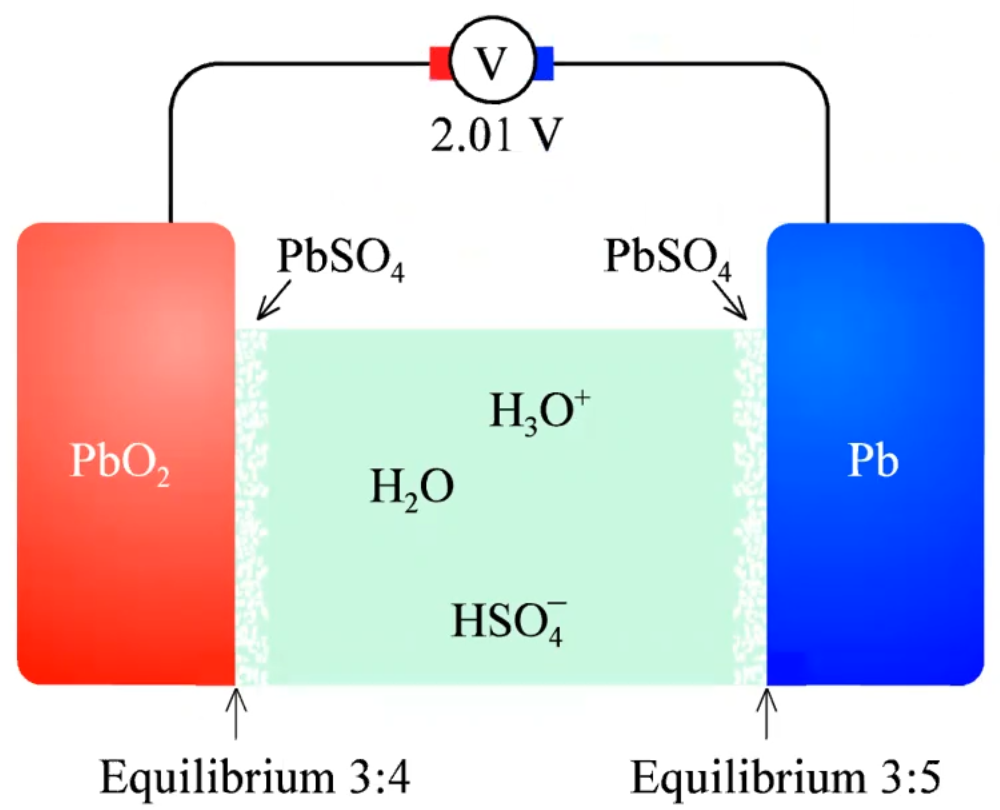Truls want us to call the positive electrode positrode and the negative electrode negatrode. Complete reaction: PbO\(_2\)(s) + Pb(s) + 2HSO\(_4^-\)(aq) + 2H\(_3\)O\(^+\)(aq) \(\leftrightarrow\) 2PbSO\(_4\)(s) + 4H\(_2\)O(l) Without thinking, you can put up the \(\Delta\)G equation, it is just determined by the activity of the products devided by the activity of the reactants: \(\Delta G = \Delta G^\circ + RT ln \left[ \frac{a_{PbSO_4}^2 a_{H_2O}^4}{a_{Pb} a_{PbO_2} a_{HSO_4^-}^2 a_{H_3O^+}^2} \right] = -375.1kJ/mol + RT ln \left[ \frac{(c^\circ)^4 a_{H_2O}^4}{\gamma_\pm^4 c_{H_3O^+}^2 c_{HSO_4^-}^2} \right]\)
- The activity of pure condensed phases is defined as unity. Hence, for instance \(a_{Pb(s)} = 1\).
- From left side to right side in eqn above: Consentration devided by standard concentration. That is why we have 4 concentrations and 4 standard concentrations.
- \(\gamma\) is the activity coefficient.
Electrical work
- w = \(\Delta\)G(J) = -ne\(\Delta\)E
- W = N\(_A\)w = \(\Delta\)G(J/mol)=-nF\(\Delta\)E
- For Lead acid batteries, 2-electron reaction: W = -2N\(_A\)Q\(_0\) \(\Delta\) E
- \(\Delta E = \frac{-\Delta G}{2F} = \frac{-(-387kJ/mol)}{2\times(96485 C/mol)}=2.01V\)
- Where the reaction energy is the real reaction energy, not the “standard one”.
- Standard(not equilibrium):
- activities = 1, can be (not required) T = 298.15k, cell votlage = 1.925V
- F = e*N\(_A\) = Faraday const.
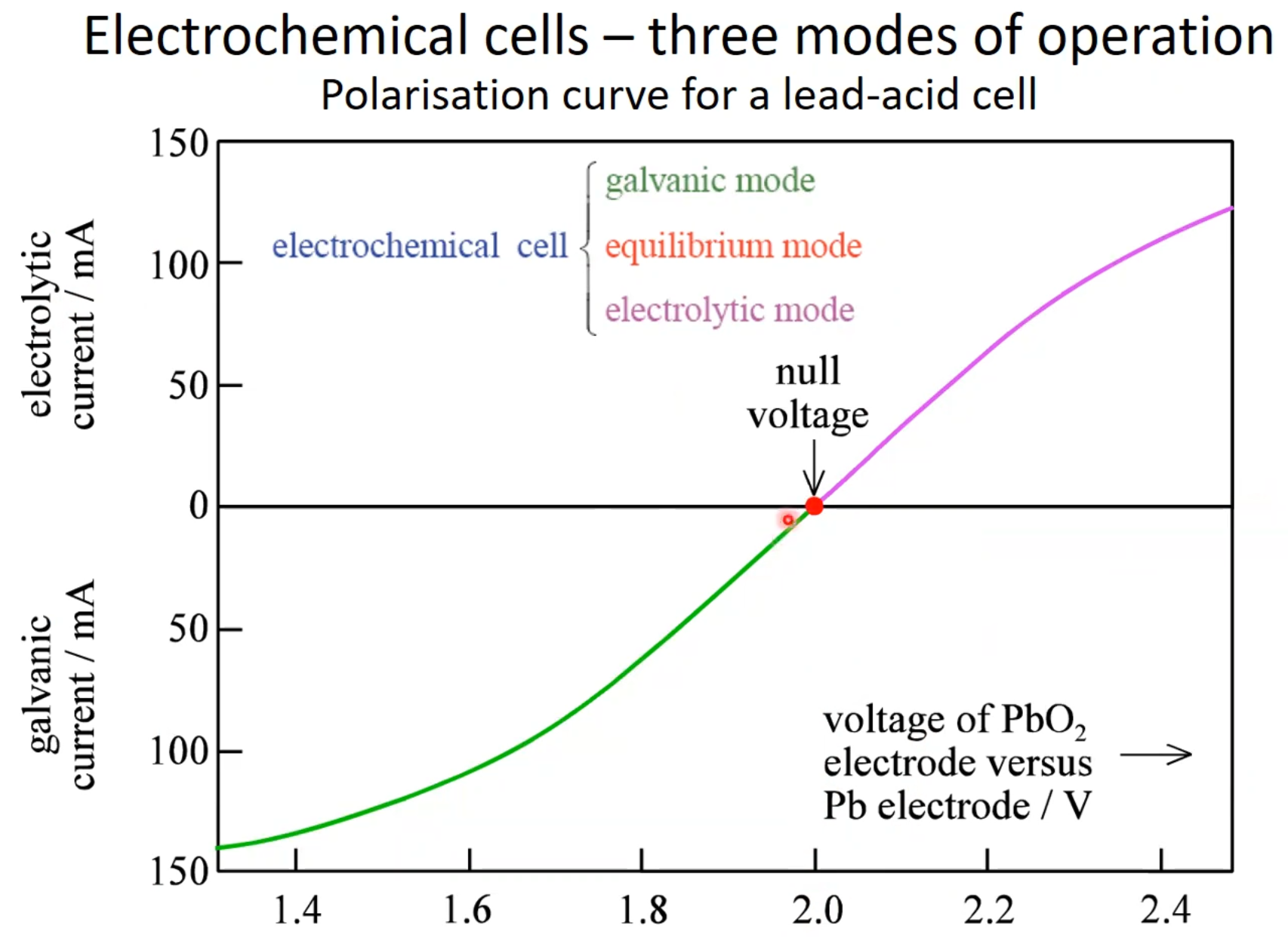
Cell usage:
Galvanic cell
- Driving force: The chemical potential differences, the spontaneous change according to \(\Delta\) G.
Electrolytic operation
- Load exchanged for a voltage source
- Electrolyzer
- Cell charging
- Cathode is suddently negatrode.
Membranes
Summary
- Galvanic operation: I>0
- Electrolytic operation: I<0
