Steady-State Electrochemistry
Equilibrium
- Concentrations are constant. Net fluxes are zero
Steady state
- Concentration gradients are constant
- concentrations are constant with time
- Net fluxes are non-zero and
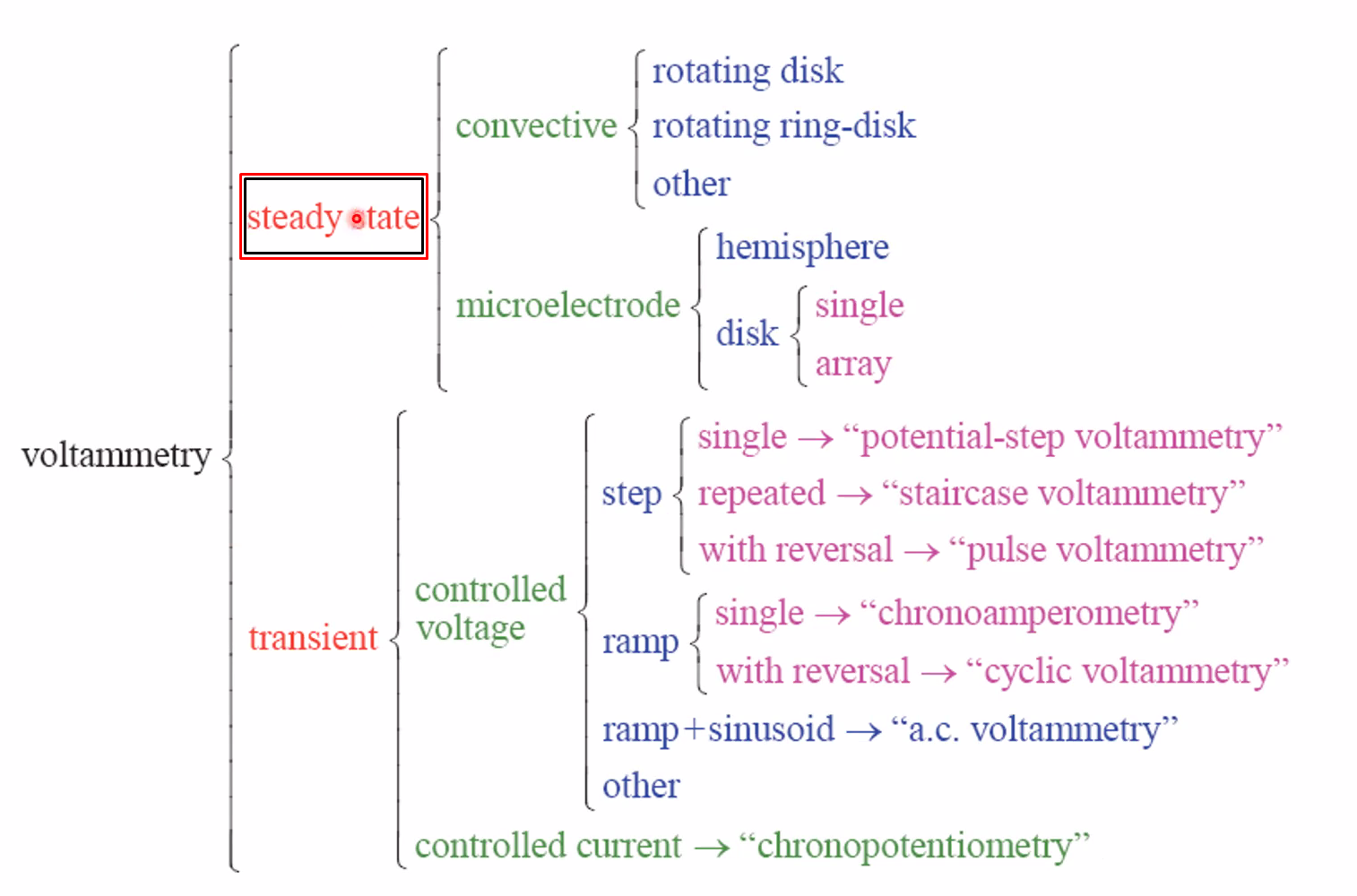
Microelectrodes and macroelectrodes
Hemispherical micro- and macroelectrodes
- Same experiment - potential leap - zero concentration at interface
- Similar simple solution
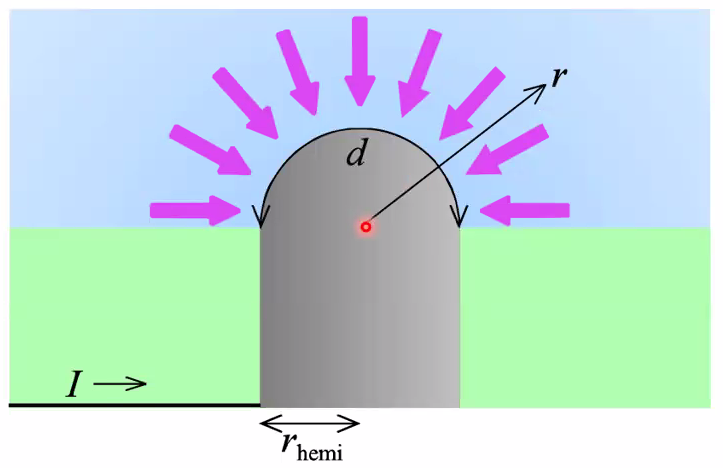
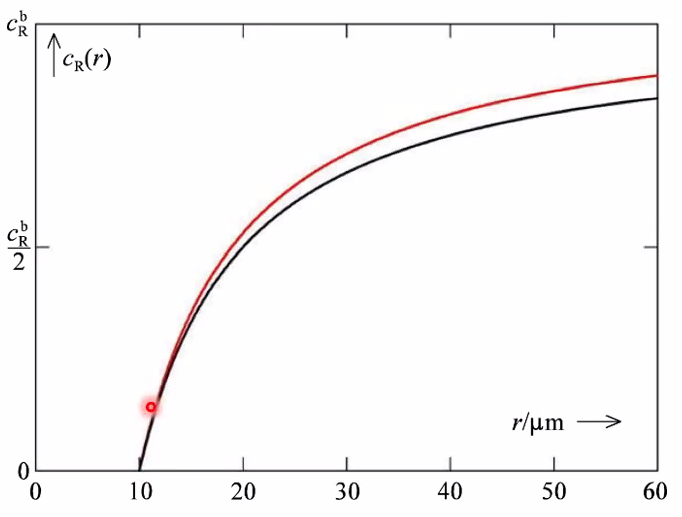
- \(c_{\mathrm{R}}(r, t)=c_{\mathrm{R}}^{\mathrm{b}}\left[1-\frac{r_{\text {hemi }}}{r} \operatorname{erfc}\left\{\frac{r-r_{\text {hemi }}}{\sqrt{4 D_{\mathrm{R}} t}}\right\}\right]\)
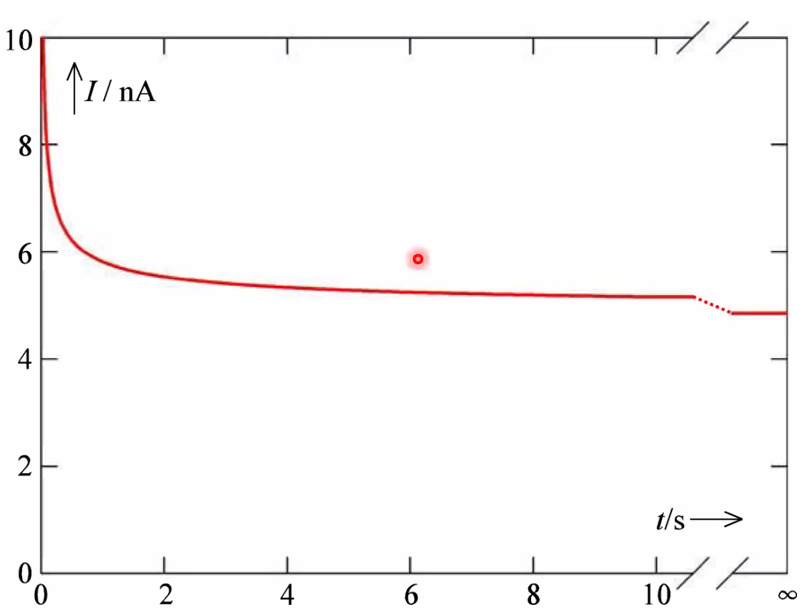
- \(I(t)=F A c_{\mathrm{R}}^{\mathrm{b}}\left[\sqrt{\frac{D_{\mathrm{R}}}{\pi t}}+\frac{D_{\mathrm{R}}}{r_{\text {hemi }}}\right]\)
- Further simplification for short times: \(I(short t) \approx FAc_R^b\sqrt{\frac{D_R}{\pi t}}, \quad t \ll \frac{r_{hemi}^2}{\pi D_R}\)
- Long times: \(I(\) long \(t) \approx \frac{F A c_{\mathrm{R}}^{b} D_{\mathrm{R}}}{r_{\text {hemi }}}=2 \pi F c_{\mathrm{R}}^{b} D_{\mathrm{R}} r_{\text {hemi }} \quad t \gg \frac{r_{\text {henii }}^{2}}{\pi D_{\mathrm{R}}}\)

Macroelectrode
- Behaves as if it were large and planar
- Diffusion controlled time dependent current
- Large electrodes may be studied as macroelectrodes up to a short time.
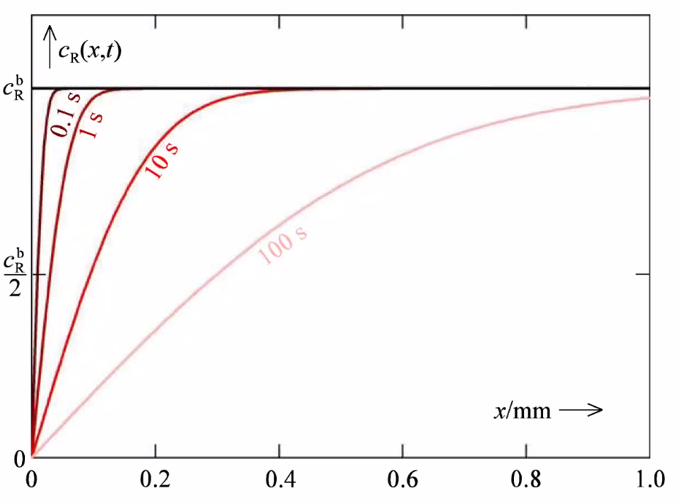
Microelectrode
- Diffusion-controlled steady-state
- Concentration gradient continues to change in the bulk, but remains constant near the electrode.
- Small electrodes may be studied as microelectrodes (steady-state) after a short time
Steady state potential step; reversibility
Previously (potential leap) looked at reactant( e.g. R) depletion
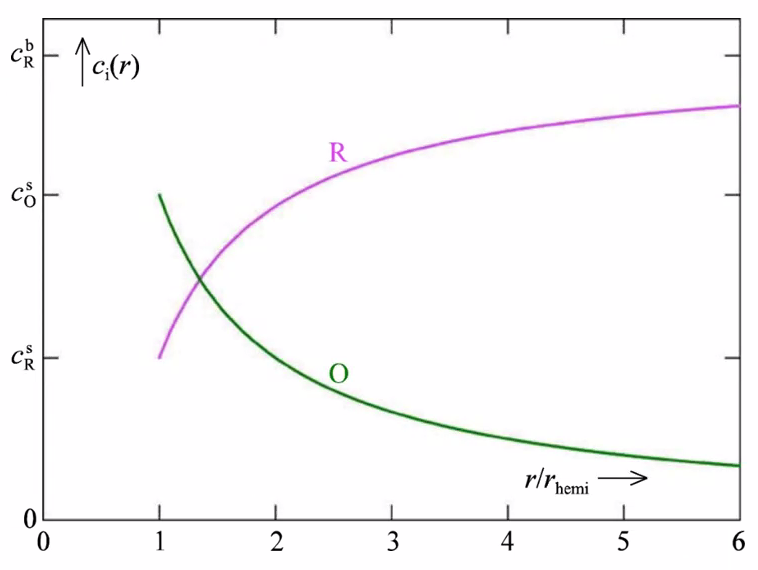
Now (potential step) also consider product (O) concentration profile
Fick’s law for both; complicated..
The book decides to consider only steady-state:
- Nernstian: \(I=\frac{2 \pi F D_{\mathrm{o}} D_{\mathrm{R}} c_{\mathrm{R}}^{b} r_{\text {hemi }}}{D_{\mathrm{O}}+D_{\mathrm{R}} \exp \left\{-F\left(E-E^{\circ^{\prime}}\right) / R T\right\}}\)
- Kinetically limited (Normal expression): \(I=\frac{2 \pi F c_{\mathrm{R}}^{\mathrm{b}} r_{\text {hemi }} \exp \left\{F\left(E-E^{\circ^{\prime}}\right) / R T\right\}}{\frac{\exp \left\{\alpha F\left(E-E^{\circ^{\prime}}\right) / R T\right\}}{k^{0^{\prime}} r_{\text {hemi }}}+\frac{1}{D_{\mathrm{o}}}+\frac{\exp \left\{F\left(E-E^{\circ^{\prime}}\right) / R T\right\}}{D_{\mathrm{R}}}}\)
- Reciprocal (harmonic) sum:
- \(\frac{1}{I}=\frac{1}{I_{\text {kin }}}+\frac{1}{I_{\text {rem }}}+\frac{1}{I_{\lim }} \quad\) where \(\left\{\begin{aligned} I_{\text {kin }} &=\frac{F A c_{\mathrm{R}}^{b} k^{\circ^{\prime}}}{\left(D_{0} / D_{R}\right)^{1-\alpha}} \exp \left\{\frac{(1-\alpha) F}{R T}\left(E-E^{\mathrm{h}}\right)\right\} \\ I_{\text {rem }} &=2 F c_{\mathrm{R}}^{b} D_{\mathrm{R}} d \exp \left\{F\left(E-E^{\mathrm{h}}\right) / R T\right\} \\ I_{\lim } &=2 F c_{\mathrm{R}}^{b} D_{\mathrm{R}} d \end{aligned}\right.\)
- \(I_{rem}\) should probably contain \(D_O\) and not \(D_R\)