Heat balance of electrochemical processes
Steam electrolisys
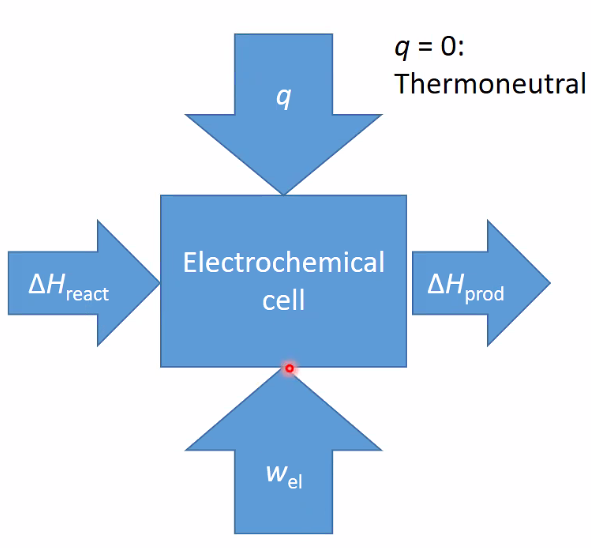
- \(\Delta H_{\text {react }}+q+w_{\text {el }}=\Delta H_{\text {prod }}\)
- \(\mathrm{H}_{2} \mathrm{O}=\mathrm{H}_{2}+1 / 2 \mathrm{O}_{2}\)
- \(\mathrm{H}_{2} \mathrm{O}(\mathrm{g})=\mathrm{H}_{2}(\mathrm{~g})+1 / 2 \mathrm{O}_{2}(\mathrm{~g})\)
- \(\mathrm{H}_{2} \mathrm{O}(l)=\mathrm{H}_{2}(\mathrm{~g})+1 / 2 \mathrm{O}_{2}(\mathrm{~g})\)
- Electrical efficiency:
- \(f_{e l}=w_{\mathrm{e}} /\left(\Delta H_{\text {react }}-\Delta H_{\text {prod }}\right)\)
- At \(q=0: w_{\mathrm{el}}=\Delta G_{\mathrm{r}}\) and \(f_{\mathrm{el}}=\Delta G_{\mathrm{r}} / \Delta H_{\mathrm{r}}\)
- \(=\left(\Delta H_{r}-T \Delta S_{r}\right) / \Delta H_{r}=1-T \Delta S_{r} / \Delta H_{r}\)
- Faradaic efficiency f\(_f\) = ratio of product rate over current
- Total efficiency f\(_t\) = f\(_{el}\) * f\(_f\)
