Electrodes
- Electrode of interest: Working electrode
- Other electrode: Counter Electrode
- Measure potential in electrolyte: Reference Electrode
Counter electrode:
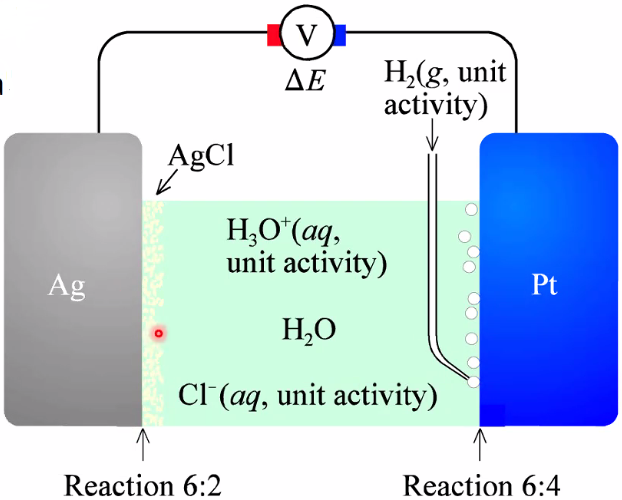
Decided standard for 0 volt: Hydrogen reference electrode
- More practical reference is Ag/AgCl electrode of 0.22V vs SHE
- Both only suitable for aqueous cells.
Working Electrode
Usually tested against a standard (SHE or Ag/AgCl)
Can find gibbs energy change from the potential from:
- \(E_{\mathrm{n}}=\Delta E_{\mathrm{n}}=\frac{-\Delta G}{n F}\)
Potentials of 1+ to 2+ ox states can not directly be calculated from potentials of 0 to 2+ and 0 to 1+. It CAN be calculated, but it includes advanced gibbs energies calculations.
Materials and geometries:
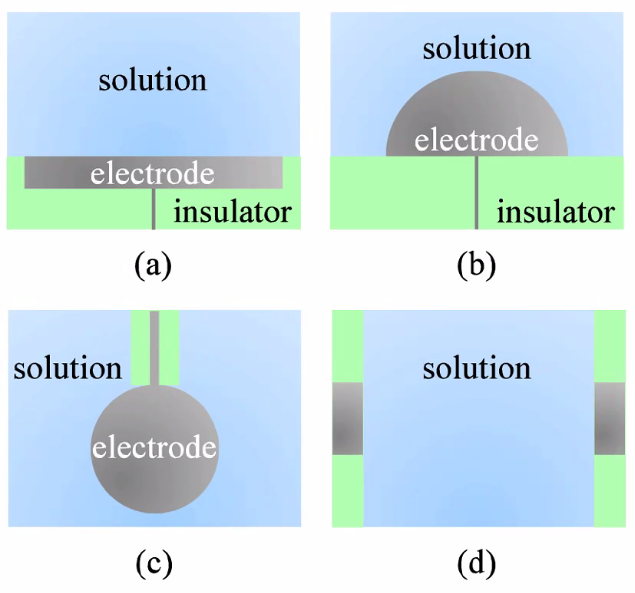
- Active VS Inert
- Active: is part of the reaction itself
- Inert: Often catalytic, Noble metals, Graphite, Glassy carbon, Oxides, Enzymes.
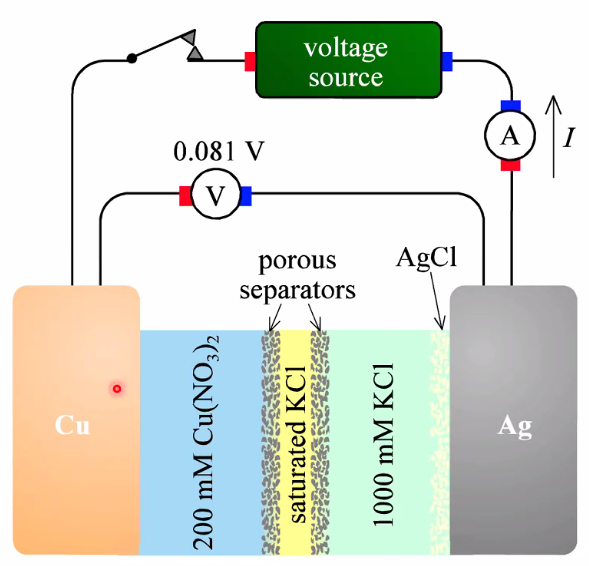
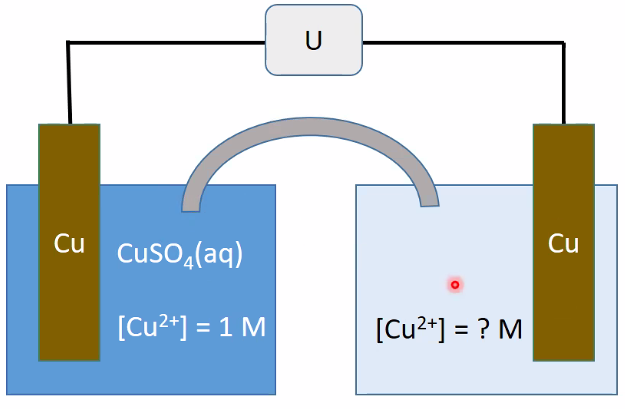
Ionic Selective Electrodes:
- Cu2+ /Cu, AgCl/Ag, but other ions can interfere alot!
- Cu:
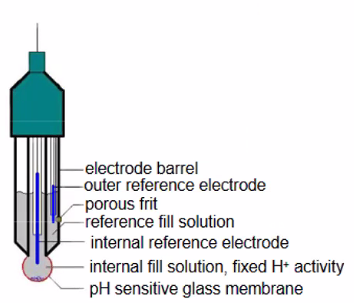
- pH electrode:
- Membrane is a protonconductor
Nernst Equation
- For cathodic, reduction, reaction: \(v_{\mathrm{A}} \mathrm{A}+v_{\mathrm{B}} \mathrm{B}+\cdots+n \mathrm{e}^{-} \rightleftarrows v_{z} \mathrm{Z}+v_{\mathrm{Y}} \mathrm{Y}+\cdots\)
- The half cell potential is: \(E=E^{\circ}-\frac{R T}{n F} \ln \left\{\frac{a_{Z}^{v_{z}} a_{\mathrm{Y}}^{v_{\mathrm{y}}} \cdots}{a_{\mathrm{A}}^{v_{\mathrm{A}}} a_{\mathrm{B}}^{v_{\mathrm{B}}} \cdots}\right\}\)
- Where the last term ( called Q) has the activities(often just consentrations) of the products on in the numerator and the activities of the reactants in the denominator. The exponential lowecase letters is the mol ratio corresponding to that reactant/product.
- Nernst eqn comes from:
- Gibbs energy change and activities change in reactions
- Scenarios:
- Std conditions: the advanced can be removed, E = E\(^\circ\) remains
- General state: It can be anything
- Equilibrium: \(\Delta\) G = 0, E = 0. Activities is such that they oppose the std gibbs energy perfectly. In this scenario, the activities become the equilibrium constant \(K\)
- \(E=E^{\circ}-\frac{2.303 R T^{\circ}}{n F} \log _{10}\left\{\frac{a_{z}^{v_{z}} a_{Y}^{v_{Y}} \cdots}{a_{A}^{v_{A}} a_{B}^{v_{B}} \cdots}\right\}=E^{\circ}-\frac{(59.159 m V)}{n} \log _{10}\left\{\frac{a_{z}^{v_{z}} a_{Y}^{v_{Y}} \cdots}{a_{A}^{v_{A}} a_{B}^{v_{3}} \cdots}\right\}\)
- natural log is exchanged to 10 log, then the value e has to be added. This is the 2.303.
- Further: 2.303 * RT\(^\circ\)/F is a constant (at room temp) which is 59.159mV
Pourbaix diagrams
- Shows cell voltage VS pH.
- For redox containing H+ or OH-
- Horizontal lines: Only redox and potential
- Vertical lines: Only acid/base chemistry
- \(\mathrm{Zn}(\mathrm{OH})_{2}(s)+2 \mathrm{H}_{3} \mathrm{O}^{+}(a q)+2 \mathrm{e}^{-} \rightleftarrows \mathrm{Zn}(s)+4 \mathrm{H}_{2} \mathrm{O}(\ell)\)
- \(E=E^{\circ}-\frac{R T^{\circ}}{2 F} \ln \left\{\frac{1}{a_{\mathrm{H}_{3} \mathrm{O}^{+}}^{2}}\right\}=E^{\circ}-(59.16 \mathrm{mV}) p \mathrm{H}\)
- Activity is exchanged for log10 and pH, since consentration of h3o+ is basically hydrogen consentration.
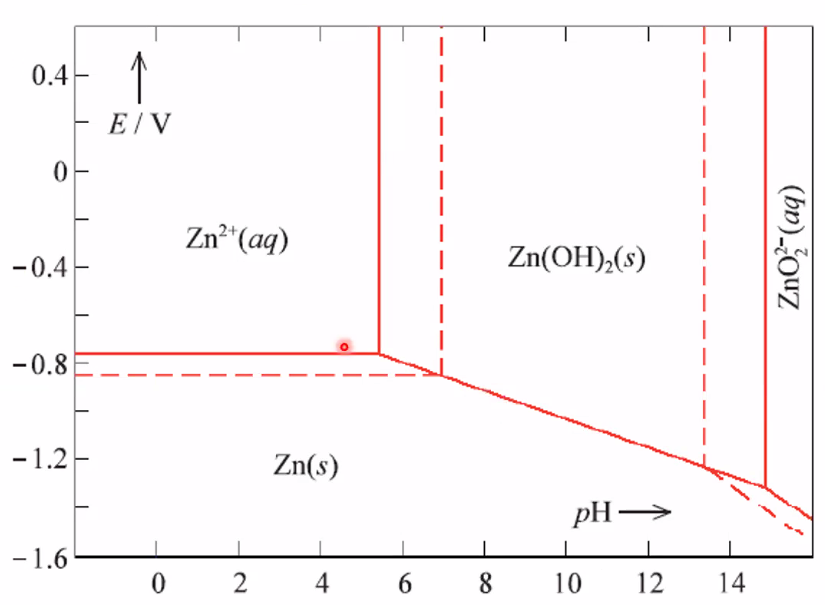
- Horizontal: Zn2+ -> Zn(s) is not dependent on pH because it doensnt include a oh-
- Vertical: Zn2+ only absorbs OH,
- Diagonals: Adic base reactions with redox reactions